I numeri-simbolo dell’indicibile del mondo: le costanti matematiche e fisiche universali

Non sono intitolato a parlare dei numeri come principio filosofico, de l’ “Uno” dei Veda, degli eleatici o di Plotino, ma, da fisico, dei numeri come strumento di interpretazione, classificazione e ordinamento del reale. Ci sono nu- meri che stringiamo nelle mani, che possediamo compiutamente, che non hanno nulla di inespresso, e questi sono i numeri naturali, 1,2,3,4…, ed i numeri razionali, ovvero frazioni formate da due numeri naturali, come 3/4, oppure 128/59, ecc. . Anche frazioni razionali complicate danno luogo a numeri perfettamente definiti perché il risultato della divisione darà, dopo la virgola, un periodo che si ripete indefinitamente. Un esempio per tutti è 71/13 = 5.461538461538461538461538…, dove il periodo è 461538.
Ma vi sono anche numeri che sfuggono alla nostra presa immediata. Indicibili, ma perfettamente definibili: sono i numeri irrazionali. Per essi non c è un periodo, ed il procedimento per definirli richiede tenacia e va comunque arrestato alla approssimazione voluta, perché coinvolgerebbe infiniti passi successivi. L’idea è quella di trovare numeri razionali, carabinieri, che stringano a destra e sinistra il malfattore. Si costruiscono cioè due successioni di numeri razionali, una maggiorante ed una minorante che si avvicinano sempre di più, per eccesso e per difetto, al valore del numero irrazionale. Per i greci il numero irrazionale e’ “inesprimibile”, ́ ̓αρρητoς, (surdus per i latini, da cui
absurdum). Numeri che nascono da costruzioni geometriche. E’ questo il caso del più famoso di tutti:

√2.

Il numero che moltiplicato per se stesso dà 2. È la lunghezza della diagonale di un quadrato di lato 1. L’ agrimensura è, nella storia, il primo ambito di applicazione dei numeri. Aγεωμε ́τρητoς μηδε`ις ει ̓σ ́ιτω: “Non entri nessuno che non conosca la geometria” era la sentenza incisa sulla porta dell’ Accademia di Platone. È qui che, quando si tratti di un numero di grande uso, occorre un simbolo. L’ attuale simbolo √, di radice quadrata, sembra debba la sua origine al monaco agostiniano luterano M. Sbafai (1486-1567). Come √2, alcuni numeri razionali carichi di significati reconditi ma non ignoti derivano da costruzioni geometriche. Esempio tipico e’ la “sezione aurea”. Prendete la successione di Leonardo Pisano detto “il Fibonacci” (nato nel 1175). Il rapporto tra un numero di Fibonacci e il suo successivo tende, al crescere del numero, al reciproco della sezione aurea 1/φ. Se dividiamo un segmento di lunghezza 1 in una parte maggiore ‘x’ ed una minore ‘1−x’,la parte ‘1−x’ sta alla parte ‘x’come ‘x’ sta ad 1[in algebra: ‘1−x:x=x:1’]. Si trova subito che ‘ x = 1/φ = (−1 + √5)/2 = 0, 6180339887’. Da questo rapporto deriva anche il pentagono regolare e la stella a cinque punte, il Drudenfuss (piede di strega) cui si attribuivano misteriosi poteri diabolici nel Medioevo in Germania, appesa sulla porta dello studio del Dottor Faust. E’ possibile ritrovare la sezione aurea non solo nella geometria ma in natura: l’allargamento e l’allungamento devono avvenire secondo una proporzione invariata e la spirale logaritmica, che viene attribuita allo scultore e architetto Fidia, si ritrova nelle conchiglie come il Nautilus. Realizza il nostro sentimento di Bellezza. Platone argomenta che “Dio geometrizza sempre”(Plutarco).

L’altro numero irrazionale il cui simbolo è noto a tutti è π, il rapporto tra circonferenza e diametro di un cerchio. Un numero irrazionale, per giunta “trascendente”, ovvero non soluzione di una equazione algebrica (al contrario di φ). Compare anche in limiti di serie convergenti:
Un altro numero simbolo è il numero di Eulero e = 2.718281828459…. È diventato un simbolo di dominio comune, da quando si parla di crescita esponenziale del contagio, intendendo un crescita più rapida di qualunque potenza. Una crescita a potenza prevede che ogni contagiato possa contagiare un numero fisso di altri individui.
Se, per es. 2 sono i contagiati da ciascun individuo infetto, il primo giorno, con in primo contagio, ci saranno 2 infetti. Il secondo giorno saranno 4 = 22, il terzo saranno 8 =23, l’ennesimo saranno 2n, (ma, per fortuna i vaccini abbassano la velocitá di crescita del contagio). Una crescita esponenziale prevede che una persona possa contagiare un numero comunque grande di individui sani, ma con una probabilità sempre più piccola. Questo dà luogo alla serie 1 + 2/1 +22 /2·1 + 23 /3·2·1 + 24 /4·3·2·1 + … = e2. Questa serie contiene tutte le infinite potenze comunque grandi (in questo caso,
di 2) e quindi cresce piu’ veloce di ogni potenza. La statistica è l’unico strumento che ci permette di analizzare e interpretare fenomeni che coinvolgono milioni di individui. E’ chiaro che sapere che la probabilità di soccombere è ad esempio, uno su un milione, non tranquillizza, sopratutto non rende giustizia al dolore del malcapitato. Si sorride sul “mezzo pollo in media a testa” perché chi muore di fame è in genere lontano dai nostri occhi. Ma la statistica è anche l’unico strumento di raziocinio che abbiamo per uno sguardo sano, rivolto alle cose della vita, dove gli attori sono tanti e tutti diversi. Il numero di Eulero incorpora ineffabili sottigliezze matematiche come quando la si definisce.

Per non parlare della sintesi rappresentabile, grazie all’unita’ immaginaria il cui simbolo e’ i, con l’identità trovata, sembra da Roger Cotes nel 1714 e ripresa da Eulero dal 1740: eiπ + 1 = 0. Sintesi che apre al muoversi lungo il cerchio goniometrico e a tutte le applicazioni della corrispondenza t ↔ ω (tempo ↔ frequenza) sviluppate per il trattamento dei segnali con la trasformazione di Fourier, fino alla radio e oltre.
E via enumerando.
Questi simboli sono ormai riconosciuti in tutto il mondo globalizzato, salvo piccole sacche di comunità isolate. Ci sono invece simboli che, per le comunità che li comprendono, sono l’immagine del nostro mondo. Il simbolo ©️ rappresenta la proprietà di un bene o di un’idea, specchio del nostro mondo capitalistico. Il simbolo @ rappresenta la rete informatica che mette in comunicazione gli individui, il cyberspazio che ci avvolge, di cui siamo noi stessi gli avatar, le incarnazioni.

I quattro giganti medievali dell’indagine su Dio, sull’anima e sul mondo, sono Averroè (1126-1198), Mosè Maimonide (1135-1204), ambedue nati coetanei a Cordova, Alberto Magno di Böllstadt (1206-1280)(detto Doctor Universalis) ed il suo discepolo Tommaso d’Aquino (1225-1274) (detto Doctor Angelicus). Essi si abbeverano alla stessa fonte: Aristotele. Per Maimonide, Dio è intelletto in atto. Per Tommaso, Dio è “l’actualitas omnium actuum”, l’attualità di ogni atto. Per Averroè, l’intelletto è pubblico, è comune a tutti gli esseri umani, agisce su di noi e garantisce le nostre relazioni nel mondo. Un pò come la grammatica universale di Noam Chomsky, innata nella specie umana.
Il quesito che nasce è se i simboli sono solo un riflesso, una rappresesentazione del reale (“nomina nuda tenemus”) o sono concettualizzazione dell’ intelletto in atto. A questo proposito, conquista recente della filosofia è che la realtà è azione (in tedesco realtà = Wirklichkeit, viene da “wirken”: agire). A fondamento della nuova fisica impostasi il secolo scorso, c’è l’ azione = energia × il tempo in cui si esplica. Il mondo è una congerie complessa di azioni: l’elettrone che gira attorno al nucleo atomico e garantisce la stabilità dell’atomo, l’elettrone che lega due atomi in

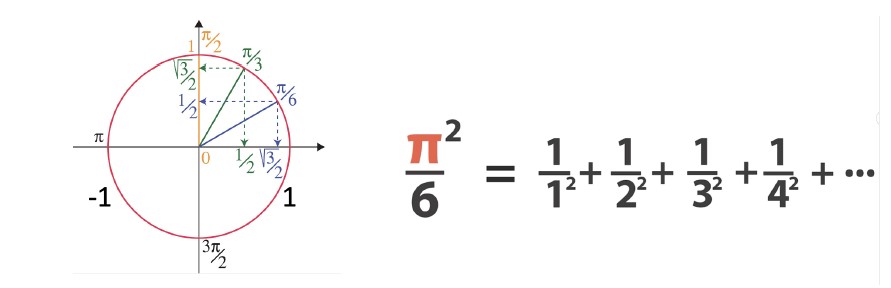
una molecola o in un materiale, la luce che incide su una superficie ed esercita una pressione, la fissione di un nucleo radioattivo, un impulso elettrico cerebrale. La cosa sconvolgente della nuova fisica è che l’azione è solo disponibile a pacchetti. Pacchetti di una azione elementare, il quanto d’azione (di Planck, 1900) ed il suo simbolo è ℏ . Questa ℏ, energia × tempo elementare, è alla base di tutte le ingegnerizzazioni della Natura e nostre. Azioni tra di noi e di noi sul mondo, con trasformazioni, non sempre prive di conseguenze nefaste. Questa azione elementare, questo quanto di azione, ha un numero: ℏ = 6.582119569… × 10−16eV · sec = 1.054571817… × 10−34Joule · sec, e questo numero, dato qui in certe unità, insieme a quelli delle altre costanti fondamentali, plasma il nostro universo inclusi noi stessi. L’interazione tra luce (di velocita’ c) e materia e’ fondamentale per la vita ed e’ governata dalla costante di struttura fine pari a e2/ℏc ≈ 1/137… , numero puro, cioè privo di unità particolari, che conosciamo con una precisione impressionante: un numero che per noi è un mistero.

I simboli sono immagine del mondo. Immagine, non rappresentazione (“Bild”, non “Vorstellung”) Come la poesia e la pittura portano l’essere in superficie per disvelarlo. Non sono icone. Averroè, nel commentare il terzo Libro del “De Anima” di Aristotele tratteggia l’intelletto “materiale” che è immateriale e pura potenzialità. È complemento della pura attualità (l’intelletto agente) realizza l’ascesa dalla esperienza sensibile agli intellegibili con l’astrazione delle forme. In questo senso è garante dell’universalità della conoscenza e della verità. Ma non è separato nel singolo individuo e non consegue quindi l’immortalità dell’anima individuale.
La disputa sull’interpretazione dei testi di Aristotele trovò felice terreno nelle nascenti Università. Intorno al 1220 Filippo il Cancelliere fu magister all’Universit‘a di Parigi e cancelliere alla cattedrale di Notre-Dame ( muore nel 1236). La lettura di Aristotele in principio non era ammessa. Significativo lo sciopero del 1229-31, di studenti parigini e docenti che si trasferirono in massa ad Oxford, dove non era proibito far lezione sui testi di Aristotele. Tommaso d’Aquino insegna a Parigi, su raccomandazione di Alberto Magno, alla Facoltà delle Arti, Universitas magistrorum et scolarium Parisiensium dal 1269 (torna a Napoli nel 1272) e confuta l’averroismo in nome di un’anima individuale immortale, con le opere:
De unitate intellectus contra averroistas, De aeternitate mundi e numerosi commenti alle opere aristoteliche:
De anima, Analitici, Politica (Secretum secretorum) – (incompiuto e terminato da Pietro d’ Alvernia), De sensu et sensato, De memoria et reminiscentia, il commento al Liber de causis (circolo di al-Kindi) e un commento, perduto, al Timeo di Platone.
Dante, era perfettamente cosciente del valore filosofico-scientifico dei protagonisti e pone Averroè nel Limbo (“Aver- rois, che ’l gran comento feo.”, Inferno, IV, v. 144) ed i suoi opponenti cristiani nel Paradiso, dove San Tommaso gli parla (Paradiso X, v. 68 e segg): …”Questi che m’è a destra più vicino, frate e maestro fummi, ed esso Alberto è di Cologna, e io Thomas d’Aquino…”.
L’enorme rilevanza della disputa è interiorizzata dalla pittura del trecento che documenta il prevalere della filosofia tomistica con dipinti ricorrenti del trionfo di S.Tommaso su Averroè. Riportiamo le foto dei più noti. Tuttavia il rinascimento farà un pò giustizia e Raffaello, nell’affresco in Vaticano, “La Scuola di Atene” (1509), ritrae Averroè che sbircia dal retro Pitagora, così, in un certo qual modo, riabilitandolo.

Tra le università appena nascenti (Parigi e Oxford, seconda metà del XII secolo), c’è anche la Scuola medica Salernitana ( IX secolo)) a completare il crogiuolo (κoινη ́) della cultura mediterranea. “Quattro sono le città che eccellono sulle altre: Parigi nelle scienze, Salerno nella medicina, Bologna nel giure ed Orleans nelle arti attoriali” (Tommaso d’Aquino nel De virtutibus et vitiis).

Ci sono eventi-simbolo come il primo concilio di Nicea (325) che redasse il Simbolum Nicenum-Costantinopolitanum, Testimonium fidei, come la discesa dell’uomo sulla Luna o l’attentato alle Torri Gemelle e simboli viventi come i testimoni. Nella foto è ritratta una sopravvissuta alla Shoah con il pontefice Francesco che bacia il numero che le fu tatuato sul braccio nel campo di sterminio. Su questo, delicato è il problema della memoria e la turpitudine del negazionismo, quando vengano a mancare i testimoni. “L’ autorità del testimone consiste nel suo poter parlare unicamente in nome di un non poter dire, cioè nel suo essere soggetto.” (G.Agamben,”quel che resta di Auschwitz”, pg.147). E’ significativo che in latino “il testimone” si dica “testis” che ha la stessa radice della parola “superstes”, superstite.

Arturo Tagliacozzo

Dipartimento di Fisica “E. Pancini”, Università degli Studi di Napoli Federico II, via Cintia, I-80126 Napoli, e INFN-Sezione di Napoli