La logica del computer quantistico e gli stati magici

di Dragut.biz · Maggio 14, 2024

Nella terza settimana di aprile si e’ tenuta la XVIII edizione della Capri Spring School on Transport in Nanostructures, curata dall’Associazione Scienza e Scuola APS, che ha luogo ad Anacapri con cadenza annuale ed è diretta a studenti di dottorato in Fisica o giovani ricercatori post dottorato nella massima parte stranieri (una quarantina). Tra gli altri contenuti (rimandiamo per tutte le informazioni alla pagina web http://capri-school.eu ), ha avuto largo spazio il quadro dello stato attuale di realizzazione e programmazione di un computer quantistico. Hanno contribuito al tema, tra altri docenti:

Pedram Roushan, di origine iraniana, leader di un team di Intelligenza Artificiale Quantistica presso Google a Santa Barbara,

Michel Devoret, che iniziò quarant’anni fa circa gli esperimenti a Parigi per la costruzione del qubit a stato solido (vedi seguito). Di recente, dopo Parigi e Yale, Devoret è stato arruolato anche lui da Google Santa Barbara di recente. Ancora, dall’Università di Santa Barbara, Sagar Vijay, una giovane promessa, laureatasi a Princeton dieci anni fa e poi transitato per l’MIT e Harvard. |1⟩11

Il qubit è il mattone essenziale per la costruzione di un computer quantistico. Quello a stato solido usa nanostrutture metalliche nello stato superconduttivo e quindi necessita di un ambiente a temperatura molto bassa (circa 1milliKelvin). Un simile ambiente lo protegge anche da rumore esterno che indurrebbe errori nel suo funzionamento.

Il qubit ha due stati possibili, come il bistabile dell’elettronica corrente ( che chiameremo “classica”), che si indicano con 0 e 1 . Ma qui il primo vantaggio della computazione quantistica: invece di avere la sola alternativa 0 o 1 per ogni bit, il qubit consente di sovrapporre i due stati e farne una miscela, una qualsivoglia combinazione. Come si può immaginare di fare una crostata con tre parti dell’impasto zuccherato e una parte con la cannella. Lo stato risultante si scriverebbe a = 3 ⋅ 0 + 1 , dove “a” designa questa particolare natura mista della crostata. Il segno + dice che si combinano tra loro i due stati 0 e 1 . Questa sovrapposizione si realizza con dei piccoli campi elettrici o magnetici applicati al qubit.

Il segno + ha però senso tra cose omogenee, gli stati dello stesso qubit: si può sommare una pera ad un’altra pera ma non ad una patata, a meno che non si astragga dalla loro natura di pera e patata e si definiscano come due oggetti senza le qualità di pera o patata. Due qubit sono oggetti indipendenti (non omogenei, come la pera e la patata) e in principio si possono al più considerare insieme, ma non mischiare. Se lo stato del primo è indicato con le lettere minuscole e quello del secondo con le lettere maiuscole, lo stato dei due qubit considerati insieme può solo essere indicato giustapponendo quelli dei due. Ad esempio: Z = a A (la doppia lineetta orizzontale a sinistra indica che questo è uno stato a due qubit, non a singolo qubit come a e A). Ma questo approccio di calcolo è ancora classico (se togliamo la “qu” al qubit e limitiamo a ed A ai soli valori 0,1 siamo in ambito classico). E, per operare sul bit a e su quello A , il computer classico, può farlo o in sequenza (calcolo sequenziale) o in parallelo (il calcolo parallelo è un modo per velocizzare, ma richiede di raddoppiare tutto il macchinario).

Qui interviene il grande vantaggio introdotto dall’entanglement, la seconda peculiarità del calcolo quantistico: legare tra loro il qubit a e A in modo che is operi contemporaneamente su ambedue. Pensiamo allo stato del primo qubit come una miscela di a e b (per esempio quella più semplice: a +b). E parimenti per il secondo qubit la miscela A +B. Non cerchiamo (a +b)( A +B), che è uno stato simile a Z , ma aA +bB oppure aB +bA . Ambedue le combinazioni sono particolari stati in entanglement. Notare che la somma delle due combinazioni riprodurrebbe la forma prodotto (a +b)( A +B), ovvero i due qubit separati e giustapposti.

L’obiettivo è realizzare l’entanglement dello stato di tutti i singoli qubit per generare un unico stato della rete ed operare su quello con un’unica operazione globale. Si può immaginare che ciò comporti un vantaggio rispetto alla sequenzialità o al parallelismo della computazione classica. Per garantire la purezza dello stato di entanglement occorre che la rete sia il più possibile protetta da perturbazioni provenienti dal suo esterno.

sala convegni

La maniera per operare sullo stato entangled è in parte analoga a quella del computer classico: con delle correntine si attivano delle connessioni tra i gate. Vi sono i gate detti “Clifford gates” che possono essere simulati anche classicamente. I gate che possono generare tutti gli altri Clifford gates sono in tutto tre: due di singolo qubit (Hadamard e phase gate S) ed uno a due qubit (CNOT). Per avre un’idea, il CNOT flippa il secondo qubit (il qubit target) se, e solo se, il primo qubit (quello di controllo) è nello stato 1 (se i qubit sono nello stato misto (+), vale la proprietà distributiva della somma ).

Questi tre gates tuttavia non realizzano entanglement. In questo senso è possibile simularli classicamente.

Supponiamo di voler realizzare lo stato entangled aA +bB. Torniamo all’esempio precedente:

(a +b)( A +B) = a A +bB + aB +bA.

Dobbiamo tagliar via le ultime due combinazioni. Il farlo è equivalente a fare una “misura classica” sullo stato, che permetta di

I computer quantistici come quello di Google richiedono un refrigeratore (vista dell’ interno) che contiene tutti i contatti elettrici ed, in basso, il processore quantistico, nella zona più fredda.
(da Google Quantum AI),

riconoscere le componenti separatamente e così eliminare quelle non gradite. Una “misura” equivale ad intervenire (in modo automatico naturalmente) dall’esterno, cosa che comunque ha conseguenze sulla coerenza quantistica della rete. Un gate particolare a due qubit, più una “misura”, chiamato gate T, svolge questo ruolo. Così si conclude la collezione di operazioni che consentono lo sviluppo di un algoritmo qualsivoglia (universalità del quantum computer). Il problema è evitare di introdurre errori e limitare il danno. Attualmente si sta cercando, con procedure preliminari, di “distillare” particolari stati già in entanglement, che possano aiutare a realizzare il gate T in modo meno laborioso ed più affidabile. Questi stati sono stati denominati “magici”.

Operazioni di misura sono anche richieste per riconoscere e correggere errori che alterano in modo non voluto lo stato durante l’evolversi del processo. Questi errori derivano in genere da rumore esterno e la individuazione e correzione comporta, di nuovo, interventi che danneggiano la coerenza quantistica dello stato globale. Al momento, una rete di 12 X 12 qubit è un buon tavolo di lavoro per avere un ottimo controllo della fedeltà nell’evoluzione dello stato quantistico a seguito degli algoritmi impiegati. Ciò non toglie che a tutt’oggi si realizzino anche reti con più di mille qubit. Un modellino di rete è riportato in figura e descritto nella didascalia a fianco.

È importante individuare gli ambiti entro i quali un computer quantistico si rivela essere superiore rispetto ad uno classico (la cosiddetta “quantum supremacy”). Ovvero, quando conviene operare con algoritmi quantistici con un numero tollerabile di errori, perchè i tempi di lavoro sono inarrivabili dai computer classici. L’ IBM ha presentato già nel 2019 a Las Vegas il primo computer commerciale, l’IBM Q System One. In quell’anno il Quantum Artificial Intelligence Lab di Google diretto da John Martinis, ha impiegato, con un processore quantistico (Sycamore di 53 qubit) circa 200 secondi per eseguire un processo quantistico un milione di volte circa. Un risultato analogo, con un computer classico, avrebbe richiesto circa 10.000 anni (Nature 574, 505 (2019)).

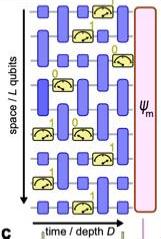A sinistra è riportato il modellino di una rete solo lineare (una catena di qubit), orientata in verticale. La direzione orizzontale rappresenta vari momenti dell’evoluzione temporale della rete. Le zone blu rappresentano qubit singoli o due qubit accoppiati.

L’esterno di Villa Rosa, Anacapri

Le icone con lancetta indicano “dispositivi di misura”. Lancetta a sinistra: si isola solo la componente 0 dello stato (per lo stato

a = 3 ⋅ 0 + 1 introdotto sopra, resta solo 3 ⋅ 0 ). Lancetta a destra: si isola solo la componente 1 dello stato. Ad esempio, al primo istante dopo l’inizio del processo (istante zero), dalla cima, si fanno interagire il 1° e 2° qubit che erano non in interazione diretta all’istante zero, lasciando a parte il 3° . Si prende poi, con un’operazione di misura, solo la compoente 0 del 4° che era in interazione col 5°, mettendo ora in interazione il 5° col 6°. Del 6°, si era conservata all’istante zero, la sola componente 1. E così procedendo. Dopo ogni operazione di misura si cerca di dare tempo al sistema perchè ricrei l’entanglement globale che la misura ha danneggiato.

In uscita c’è lo stato totale finale ψ_m che va “letto” ed è l’esito del calcolo. (da Google Quantum AI and Collaborators, Nature 622, 481-486 (2023))